Spatial
Dynamics of Human Populations: Some Basic Models
Robert A. Hanneman
(robert.hanneman@ucr.edu)
Department of Sociology
University of California, Riverside
2005
For a
translation in French by Kate Bondereva please
see: http://www.autoteiledirekt.de/science/dynamique-spatiale-des-populations-humaines-certains-models-de-base
Introduction
This small project grew out
of my frustration in trying to integrate my early work, based on self-training
in "systems dynamics," with newer and emerging work based on
"complex systems" and "agent-based" modeling.
"Systems dynamics"
is a particular "school" of social science approaches to the
application of non-linear differential equation modeling. This tradition
has a rich tool-kit for understanding, by modeling and simulation experiments,
systems that tend to be fairly complicated in terms of numbers of variables and
complicated functional relations among them. But, the tradition has a
strong bias towards conceiving problems as "closed systems," and the
thinking is largely "top-down."
In recent years, more of the
social science modeling community has become engaged with
"agent-based" approaches, linked closely to the growth of interest in
"complexity" and "emergence." Models of this general
type are "bottom-up" and see macro patterns as emerging out of the bounded
and locally directed actions of numbers of coupled actors. The actors (or
sub-systems, or agents) are usually approached as minimally complex in
themselves (often limited to having one or two categorical attributes and
simple action rules). The complex dynamic behavior of is the consequence
of the coupling topology of the agents.
At the most basic level,
there is no difference between the two approaches. "Systems"
are often usefully treated as composed of multiple interacting
"sub-systems." That is, many systems models are not
first-order, and can (and do) display complex dynamics. Similarly, one
can easily think of agents as "sub-systems." Which emphasis is
most useful is likely to depend on the problem; agent models tend to give
us better leverage over problems dealing with emergence (and possibly
evolution) of coupling topology; systems models tend to give us better leverage
over understanding the range-of-motion and historical dynamics types of
problems.
As a macro-sociologist, my
primary interests are in the dynamics and evolution of moderately large scale
systems (communities, organizations, classes, societies). It is usually
the case that "agents" of these types need to have fairly large
numbers of attributes (variables), and often rather complicated (non-linear,
lagged, contingent) rules that describe their behavior. Those needs
pre-dispose the macro-modeler to a systems approach. But, it is also very
clear that the coupling of multiple interacting macro agents is critical (my
other main field of study is social networks). The dynamics of
communities are affected by their adjacency to other communities; the internal
dynamics of nation states are affected by the way that they are embedded in
systems with other nation states. There are often moderately large
numbers of agents in explicit macro-models, and the topologies of their
coupling can be complex. These sorts of issues pre-dispose the modeler to
agent-based approaches.
In the models that are
developed in this text, we begin to bring together the two traditions together,
as they apply to macro-sociological dynamics. We will work with several
macro theories relating to demographic, ecological, and political economic
processes. These theories are expressed as non-linear differential equation
models describing the internal dynamics of an agent. We will then
couple a number of these complex agents into a macro system. We conceive
of the coupling of agents as "spatial," and consequently also draw
some direction from physical systems modeling traditions in ecology and
geography. Models of social dynamics, however, require flexible and
multiple conceptions of "space." Most notably, social network
analysis provides ways of conceptualizing the coupling typologies of complex
social systems in ways that may be thought of as "social
space."
The distances between, and connections
among social actors (people, families, communities, organizations,
sub-populations) are obviously important in conditioning many forms of social
action. In many areas of the social sciences, distance and connection
regularly figure into models of dynamics (E.g. demography and ecology, network
analysis). Many important theories in the social sciences, though, pay
remarkably little attention to space - or treat space as an annoying
"disturbance."
In many ways, this is like theorizing
principles of the dynamics of physical interaction assuming "a perfect
vacuum" and "frictionless surfaces." These are useful
assumptions to get at the core theoretical principles, but obvious limitations
from a practical engineering point of view. More troubling is the
possibility that ignoring or over-simplifying the distances and connections
among social actors is rather like attempting to reduce the dynamics of
molecular interaction to the attributes of atoms. This doesn't work, even
in theory.
Assuming that distance
doesn't matter in social relations may be reasonable for some dynamics -- if
all we seek to understand is theoretical equilibrium outcomes; but distance can
matter a great deal for any practical applications of social theories.
But many social phenomena may be embedded in space in ways that can't be
ignored, even in the abstract. The properties and dynamics of social
structures may emerge in non-linear ways from the "coupling topology"
or "connectedness" of the parts.
Our goal, of course, is
useful general theory of social action. Distance and connection may be
boundary conditions or explicit terms in such theories, or they may be core
concepts. To build theories that take distance and connection seriously,
a very good strategy is to move back-and-forth between our developing theory
and analytic models that are explicitly linked to them. One goal of the
project is to try to bring distance and connection issues more explicitly into
some very basic social theories.
This is not a new, or unique enterprise. There are very large and
excellent literatures that do take the role of distance seriously in social
dynamics. We may be add a brick or two to that wall, but the main goal is
to try to engage more social scientists to begin to think about, and to play
with spatial dynamics in a wider range of sub-fields and applications.
There are a number of
important and useful social-science macro models that do involve multiple
complex agents, coupled together (for example: International
Futures). There are also a number of excellent agent-based models that
involve multiple agents (e.g. Sugarscape).
Building models of these types has, until recently, been a major undertaking --
as most such models were developed directly using high-level languages.
Most social scientists (unfortunately) have very limited training in
programming and the fairly basic mathematics that are necessary to develop and
experiment with either systems or agent models.
Friendly and accessible
software tools do exist for both systems modeling (e.g. Stella, Madonna, Vensim, add others) and for agent modeling (e.g. Logo,
Swarm, RePast, and others). Developing models
of any complexity in these environments, is tedious, and does require a good
bit of learning. But software work-benches like these do make modeling
accessible to most social scientists. The models that we present in the
pages of this site are developed to run in the Berkeley Madonna environment.
The code for the algorithms has been made as simple, transparent, and portable
as possible. The Madonna software environment is available free for
viewing models (and is very inexpensive for a full version). We
settled on Madonna as our platform because it has very nice input, output, and
graphing tools, a simple syntax for writing programs, useful libraries of
functions, and support for one and two dimensional arrays -- which are
essential for building spatial models.
What Madonna did not have,
that we needed for our application, are tools for handling complex coupling
topologies among large numbers of agents. Our primary contribution at the
technical level is that we have developed fairly simple and portable modules of
code that can be used to deal with some common coupling topologies necessary
for macro-models: neighborhoods, distances, and network adjacency.
The array handling of Madonna can deal with large numbers of internally complex
agents. We've added some tools for handling some of the coupling
together of large numbers of agents. Our goal is to make it easier to
develop models of complex agents embedded in complex spaces, without having to
write lots of code.
The code,
in Madonna, for all the models in this site are downloadable from the
pages of the site. In most cases, the code itself is quite simple, and we
have tried to provide sufficient documentation with comments to understand what
the programs are doing. By using the Madonna environment and just a bit
of programming, most models can be stated in surprisingly few lines of
code. Our goal, of course, is to urge you to play with and modify the
code in ways that you find interesting and useful.
The notion of expressing
theories as formal mathematical models of dynamics is commonplace in most of
the physical and life sciences. It is not so common in the social
sciences. This is unfortunate, and can create a sort of a "language
barrier" between parts of the scientific community. But increasing
numbers of social scientists are coming to understand, appreciate, and adopt
these tools; and there is a continuing flow of personnel and ideas from the
physical and life sciences into social science fields and into
interdisciplinary efforts such as the Santa Fe Institute.
One of our goals was to
increase the stock of fairly easy-to-use tools for teaching about dynamics that
"speak to" social scientists. This is hardly a unique or new
goal. Mathematical social scientists have provided very useful texts from
time-to-time (in Sociology, some exemplars are works by Farraro,
Leik and Meeker, Coleman, Lave and March).
Hands-on modeling tools and theory-informed teaching simulations have also been
around for some time. A very notable early effort in Sociology is William
Sims Bainbridge's Sociology Laboratory. More recently, several
inter-disciplinary modeling communities have made very serious and useful efforts
to provide tools and exemplars that speak directly to social science curricula
(e.g. Ruth and Hannon's Modeling Dynamic ... Systems volumes, Logo, RePast, and Swarm).
We share with these authors
the idea that the toolkit of all social scientists ought to include an
appreciation of systems and agent modeling -- even if many social scientists
will rarely do their main work using these tools. By making more tools
available that can be used in basic instruction in theory (and maybe particular
substantive fields) we hope to further encourage efforts to make work of this
type "normal" in the social sciences. The models here are not a
"course." But they may be useful
in introducing some basic ideas and tools for thinking about the role of
distance and connectivity in social science theorizing. The particular
themes of distance and connection are not a
commonplace in existing curriculum support materials for the social sciences
(though many of the existing works do address some of the same issues).
To be entirely honest, there is
no clear single logical order that organizes most of the materials in the pages
of this web-site. Indeed, we hope that more short modules will be
developed as interesting problems occur to users who want to share them here.
You will probably want to do
two things first, and then sample from the rest as it suits you.
Look through the
"Getting started" material on the remainder of this page. We'll
provide some basic information on how to work with the software and models in
the other pages.
Then, look at the page on
"Single Population Spatial Dynamics." That
page, and the attached models, explain our basic conceptual approach to
"space." It also develops the basic algorithms for handling
neighborhoods, distances, and networks that we will apply in the substantive
examples on other pages.
Then, if you're still with
us, there is no real order. Each page is intended to deal with a set of
closely related issues, but there is no real linear order among the pages
themselves.
All of the models that we discuss
on the pages in this site can be downloaded (they are all very small
files). They are in .mmd format, and are
designed for use with the Berkeley Madonna simulation environment.
You may download a version of Madonna that will enable you to view and
experiment with models for free. To create models, however, you will need
to purchase the software (student version is $99).
You can download the software
from the Berkeley Madonna website:
http://www.berkeleymadonna.com/
There is a graphic flow-chart
editing tool that requires Java to use. We won't use this tool.
If you want to know more, you
may wish to take a look at the user's manual:
Berkeley
Madonna User's Manual
The graphic below shows a
screen shot of the user interface of the Madonna environment (Windows version).

Models are built and modified
in the equation window, and use a fairly natural language. A considerable library of functions are available.
Results are produced in charts and tables. Tabular data can be
exported. Our graphic also shows a simulation control window.
The environment has excellent
tools for experimenting with models by varying parameters, and doing multiple
runs (either for random starting conditions, or to examine the sensitivity of
the models across ranges of parameters).
One feature of Madonna is
rather useful for the kinds of spatial models that we will be building.
This is the ability to input parameters and initial conditions from external
files. Suppose that we were building a model of the movements of a human
population and an animal population over space (the predator-prey model that
we'll examine in detail on another page). We will create populations of
predators (humans) and prey in each of nine spatial areas, arranged as a square
grid. One might, of course, want to create much larger environments (say
100 by 100).
To provide the values of the
number of predators and number of prey in each of the 9 squares at the
beginning of the simulation, we could write just a little code in
Madonna. It is probably easier to visualize, and to implement this by
building a "map" of the starting values we'd like. The next
figure shows a screen shot of an Excel spreadsheet (notice that the sheet has
been saved as a .csv file, not an Excel worksheet).
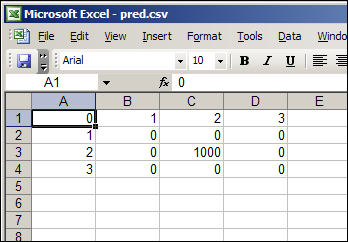
The first row and column are
used to provide index numbers to identify the locations of the nine spatial
areas. The values in the inner cells provide the starting values for (in
this case) the number of predators. In the example, we've indicated as
starting population of 1000 predators, all concentrated in the center of the
space. Multiple files are used to initialize multiple variables, as
needed.
Once the initial value map
has been created, there are two additional steps. First, a little program
code is written to call for the file. Here's an example.

The first line is a
comment. The second line indicates that we are initializing the variable
"pred_tmp" across a two-dimensional array
that has the dimensions "begin..end" by
"begin..end." The values of
"begin" and "end" are set elsewhere in the program at
"1" and "3" (in this case) to create a 3 by 3 grid.
This square array, we tell the program, is to be filled with data from an
external file (#) named "pred" (the one we
created above). The external file is to be read with the row (i) and column (j) indexes reversed. This last little
bit is peculiar -- for some reason, Madonna indexes the data array by columns
and rows. We want our external data files to look like the row by column
map of the space we are building -- so a translation is needed.
In the example, we also call
for another file to initialized the number of prey
across the nine grid squares.
Once this code is in place,
we need to tell Madonna (you only need to do this once) where to find the data,
and to load it. This is done from the menu File>Import
data set. Use the browser to locate the spreadsheet file, and
select it.
The dialog below will appear.

Since we are importing a set of
initial values that we want read as a two-dimensional array, we've selected the
radio button "Matrix (2D)." You can use exactly the same method
to import one or more vectors into your model -- which is sometimes useful for
setting parameters and other initialization tasks.
Once you've created or opened
the model's equations, and loaded the external data files (if any), you can use
the tools of the simulation environment to experiment with the model, producing
line chart and table output. The table output can be exported for use in
other programs.
Madonna doesn't have a
"map" like grid display for output -- this is an unfortunate
limitation for the kinds of models that we want to build. We're still
working on this problem, and hope to either make a tool or find one that will
allow graphical presentation variables in square matrix form -- preferably with
animation.
This is quite enough for now,
and enough to get you started. Look at a few pages of this site, glance
through the user's manual. Look at the code for a few of our
models. I think you'll find that it will not be difficult to learn an
master the necessary skills for creating useful models in Madonna, and using it's simulation environment to experiment with them.
We're not promising that it is no work; but we do think that this is much
easier than most of the alternatives currently available for building spatial
models.