Spatial Dynamics of Human Populations: Some Basic Models
Robert A. Hanneman
(robert.hanneman@ucr.edu)
Department of Sociology
University of California, Riverside
Jason Martinez
California State University
San Bernardino
2005
Game of "Life" models of infection/diffusion; mutualism/competition
Some of the most important and enduring problems is social-spatial analysis deal with how a qualitative attribute of an actor changes in response to the attributes of it's neighbors. The spread of material states (e.g. illness) or informational states (e.g. aware or unaware of an innovation, recruited or not recruited to a social movement) from actor to actor are critical social dynamics. Social movements, cultural diffusion, social learning and influence, and collective behavior all can be seen as processes where the state (and change of state) of an individual actor is affected by the states of the other actors in the neighborhood in which they are embedded.
Analogous problems have been of considerable interest to non-social scientists for some time. The model that we will study in this page was originally an attempt to understand and model the growth/extinction of bacteria in a culture medium. Bacteria spread by reproducing to new locations adjacent to their current ones -- but will only be able to do so if there is a certain density of organisms present. But, if too many organisms are present in dense clusters, "crowding" will result in the death of some. That is, the chance that a particular location has a live organism occupying it is dynamically dependent on the density of organisms present in it's neighborhood. In ecology, "patch dynamics" deals with similar phenomena. A pest may spread to a new area only if it has built up a certain degree of density adjacent to that area. But, if the overall density of pests in a neighborhood becomes very high, some will die due to crowding. If one watches a time map of the locations of insect swarms, for example, this kind of density-dependent movement of the swarms through physical space is often apparent.
The spread of ideas, activation into social movements, mobilization of allies for conflict, and other processes have some similarity to these biological and ecological processes. There are also important ways in which human social dynamics in neighborhood space differ from biological and ecological dynamics. The similarities are great enough to see what we might learn by applying these neighborhood spatial models as ways of formalizing theories of human activity.
In the first section below we will explain the game of "Life" model as it was originally developed (in the 1960s!). The game is very, very simple. Yet, it captures some quite important basic principals that apply to human behavior as it occurs in space; and the very simple game of "Life" model produces some quite remarkable patterns of emergent organization that mimic the formation and dissolution of human groups.
In the second section below we make a simple extension on the original game. "Life" was developed for von Neuman neighborhoods (i.e. actors have four neighbors -- north, south, east, and west). In this section we develop the game for the more "fine grained" Moore neighborhood (i.e. actors have eight neighbors).
In the third section below, we modify the game so that it is "played" on a network (actually, the von Neuman and Moore versions are also being played on networks -- but of a particularly restricted kind - lattices). Sometimes social action processes are well understood with physical space lattice models. The activation of people in a crowd, for example, has been studied with this sort of model by sociologists. But, many patterns of diffusion and social change occur along social networks -- social space, rather than physical space. Adapting the game of life model to this kind of "connection topology" is an area that is just beginning to be explored.
In the final section, we'll spend a little bit of time thinking about ways in which the models developed here (particularly the network model) might be pushed further to provide more realistic and useful formalizations of theories of social change via neighborhood diffusion.
table of contentsThe original game of "Life" was developed by a fellow by the name of Conway in the 1960's. The game is a formalization of two notions of "density dependence" of growth. The ideas are both very simple, and very, very important in biological and ecological systems. The ideas of "density dependence" have been borrowed -- with more or less formality and rigor -- in the study of human communities within urban places, systems of urban places, and populations of formal and voluntary organizations. So the notions of "density dependent" growth and failure are familiar in many areas of sociological theory.
Here are the two basic ideas of "density dependence:" 1) the likelihood that a new individual will be born, or that a living individual will remain alive is a positive function of the density of the neighborhood, but... 2) beyond a threshold of density in the neighborhood, competition for resources will increase the likelihood that a living individual will die, or that a birth will not occur.
We might call the first part of this "mutualism." Actually, this term is usually used to refer to the effect of the density of one species on the carrying capacity for another, but here we'll use it to capture the idea that the likelihood that a person gets converted, an organization gets mobilized, or that they sustain their belief or mobilization is a positive function of the amount of support from their neighbors. In many social situations, it seems that agents are more likely to become like their neighbors (and are less likely to become deviant if they are already like their neighbors) the more of their neighbors share a trait in common. Pressures for conformity, norms of mutual support among members of homogeneous populations, and other sorts of social dynamics predict a positive density dependence on the local neighborhood.
We might call the second part of the density dependence theory a "competition" effect. While having more neighbors who are like you may support your identity, it may also be oppressive, or limit your opportunities. You may find that living in a neighborhood where everyone is the same is boring -- and you might seek to distinguish yourself by deliberately deviating from the norm. Or it could be that your ability to maintain and prosper in a social identity or role can be made more difficult by having too many others around you who are competing for the same recognition and resources. This leads us to the idea that, sometimes, having too many neighbors who are like an actor may cause that actor to change their status to become un-like their neighbors.
A Madonna "Game of Life" Model
Conway's game of "Life" consists of a square lattice, with each node or square being either dead (zero) or alive (one). At each point in time, each node looks at it's von Neuman neighbors (i.e. the squares to it's left, right, above, and below). If the density of "alive" actors is below a threshold value, then the focal node "dies" if it is currently alive, or remains "dead" if it is currently dead. If the density in the neighborhood is at a threshold level, then the focal node is "born" (if it was "dead"), or remains "alive." If the density in the neighborhood is above a cut-off level, the focal node "dies" (if it was alive), or remains "dead."
When the game is played -- that is, the rules are applied over and over to mimic "generations" of organisms, a wide variety of (often) interesting spatial behavior "emerges," depending on the initial conditions (the model here is entirely deterministic -- though it need not be). In some cases, agents "join" to create more-or-less permanent groups; sometimes the groups "migrate" across space. The relationship between the equilibrium result (if there is one) and the initial density and distribution in space is very complex. The model displays both "emergent" structures and extreme dependence on initial conditions -- two hallmarks of "complex" dynamics.
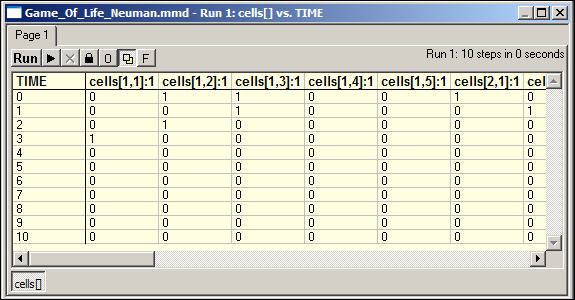
In Figure 1 we show some of the results, in numerical form (sorry, we don't have a good animated graphics routine, yet).
Figure 1. Numerical display of a von Neuman game of Life run

Madonna code for the von Neuman version of the "Life" game
Initial values file for the von Neuman version of the "Life" game
For this example, we've used a grid of five by five squares. The density dependence rules are set in a block of code near the beginning of the program (you can experiment with different theories of density dependence). For our run, the rules are: For corner cells one live neighbor is needed for survival or birth; for edge cells two live neighbors are needed; for other cells three live neighbors are needed.
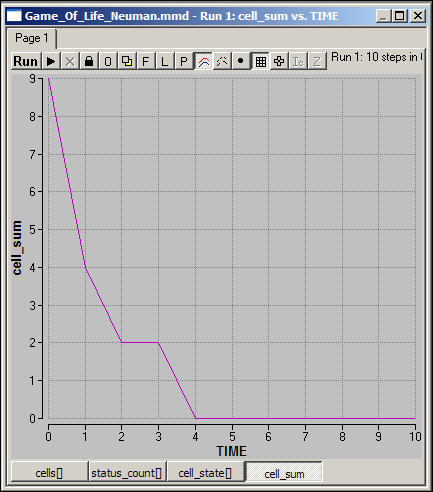
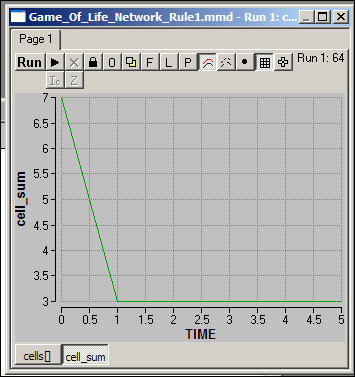
In our example, the population is extinguished after a short period of time, as we see in figure 2.
Figure 2. Density in a run of a von Neuman game of Life
You should experiment with neighborhoods of different sizes (change the parameters of "begin" and "end" in the Madonna program), and different initial densities and spatial dispersions (e.g. one initial cluster in a corner, or in the middle, two clusters, random scatters, etc.). To modify the initial configurations, create comma delimited files of zeros and ones (see the file used for our example) and load them as initialization data into the program.
Because of the limitations of the graphics in Madonna, it is rather difficult to see some of the most interesting properties of the "Game of Life." As with many dynamic models, the most interesting and provocative implications of the theory lie in the way that the behavior unfolds through time -- rather than the equilibrium tendencies (if any) of the system.
This is true with the "Game of Life." The most interesting aspects of the model's behavior are in the shifting sizes, shapes, and spatial locations of live populations through time. So that you can experiment with this aspect of the theory, Jason Martinez has adapted a version of the "Game of Life" model originally developed by Ala Qumsieh (2001, posted at: http://aspn.activestate.com/ASPN/Mail/Message/perl-AI/758384 ). The model is written in Perl, and we provide it here as an executable (.exe) file compiled for Windows.
Figure 3 shows an example of a random start for the model (each run will be different).
Figure 3. Early iteration of a random game from the Martinez adaptation of Qumsieh's model.
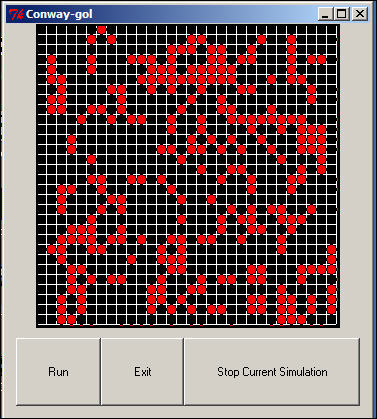
The red squares are "alive," and the black squares "dead." At each iteration, a random square is chosen, and the density/competition death and adjacent neighbors birth rules applied.
Figures 4 and 5 show the same model, but after a few iterations, and then again after a large number of iterations.
Figure 4. Mid-point iteration of a random game from the Martinez adaptation of Qumsieh's model.
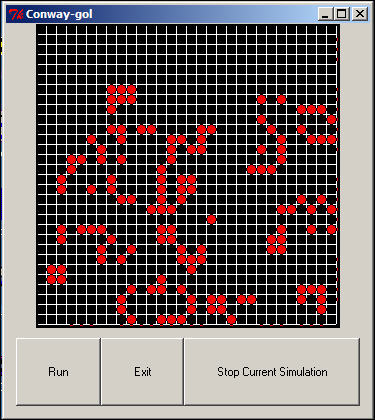
Notice that the density has decreased, and that a number of spatially separated clusters have formed. Interestingly, these clusters will often be "move" across the grid.
Figure 5. Equilibrium of a random game from the Martinez adaptation of Qumsieh's model.
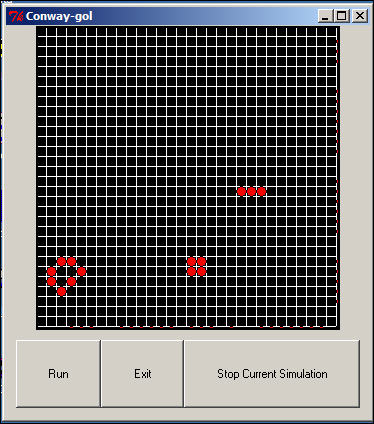
For many initial values, the "Game of Life" reaches an equilibrium of several spatially isolated small clusters, as it does in this example. Sometimes the equilibrium is stable (i.e. the points don't change at all from iteration to iteration), sometimes the equilibrium is a "limit cycle" (i.e. the patterns change, but move through a regular sequence. In this example, the cluster at the upper right (the horizontal bar of 3 live cells) "rotates" around it's central point.
Download the executable for the program
Some things to think about
Questions about the behavior of the model:
Don't be frustrated in you can't answer these questions with any certainty. If you can, though, you should publish your results!
Questions about applying the model:
Now that we've got the basic ideas, let's make a few modifications of the model.
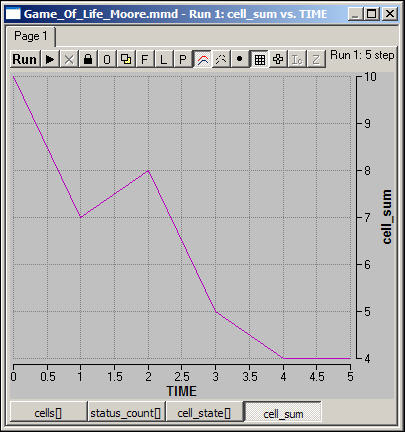
table of contentsWhat happens with a more fine-grained or more complicated neighborhood -- but one that still has a fixed lattice like structure? Figure 6 shows the density of population for one game played on a 5-by-5 grid with an initially quite high density.
Here we've used some "liberal" survival rules. Corners need only one alive neighbor, edges only two, and central squares between 4 and 6 neighbors to live. Figure 6 shows a run of the model with a Moore neighborhood and these Life rules.
Figure 6. Density in a game of Life in Moore neighborhoods
Madonna code for the Moore neighborhood game of Life
Initial values for the Moore neighborhood game of Life
In most scenarios, when played on a small grid, the game of Life results in the extinction or stability of the population after a fairly short period of time.
Often more interesting than the ultimate equilibrium (or not) of the game of Life, are the emergence of patterns as the game progresses. In some cases, small clusters of cells will appear to form, and will migrate across the grid as crowding on one edge of the "community" is coupled with "births" on another edge. Unfortunately, we haven't yet developed a good tool for the display of these kinds of patterns.
table of contentsThe spread of beliefs through a population, the development of collective behavior (e.g. "booms" and "fads"), and the diffusion of disease (e.g. AIDS) are part of a large class of similar problems that are of great interest to social scientists. All of these phenomena display some similarity to the game of Life. In a "craze" for example, normally calm and rational people may be "caught up" in a mass emotional outburst that sweeps through a crowd, and then dies out (like a "wave" in the audience at a sporting event).
In phenomena like these, actors are "mobilized" or "activated" when it becomes "normal" in their local neighborhoods to do so. That is, when some number or proportion of the neighbors of each actor are "turned on," the focal actor becomes "turned-on." Most local excitements in social structures, though, don't seem to generate movements or mobilizations that spread very far. As Watts notes in his book Six Degrees, most potential fads, crazes, and collective behaviors fail quickly, and don't diffuse very far. But, every once and a while, one does -- social revolutions occur, global pandemics result. What determines which phenomena explode, and which fizzle is mostly the ways in which actors are coupled together in social space (actually, it's not quite that simple).
It's possible to adapt the game of Life kind of model to operate in "social space" or on a network of arbitrary form, rather than on a square lattice. In this form of the game, each actor surveys the status of the actors to whom they have a connection (their network neighbors). When low proportions of the neighbors are "on," ego remains "off" or turns off. When the proportion of neighbors who are "on" passes a threshold value (say 50%), then ego turns on (or, if ego is on, it remains on).
Figure 7 shows a network of 16 actors that was created by using a 4-by-4 grid. Actors who are "on" are colored in red, those that are "off" are colored in blue. The network topology is a variation of a "small world" network in which most actors are connected in dense, but closed neighborhoods (two cliques in the upper left and lower right) and two stars (upper right and lower left). The local clusters are connected by an inner network (22, 23, 32, 33) that happens to have the form of a circle.
Figure 7. Input network structure and initial "live" cells
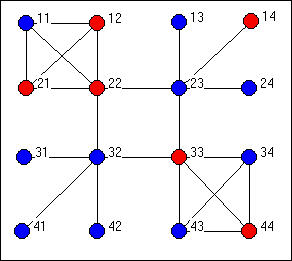
The simulation of this network produces the trend in density of "on" nodes shown in figure 8 (actually, there is an error in the graphic in figure 7 -- it should also show node 41 as "on").
Figure 8. Count of cells alive in the network Life game
Madonna program for network game of Life in figure 5
Input cell initialization for network game of Life in figure 5
Input network topology for network game of Life in figure 5
In this example, the initial density is moderately high (7 of 16 cells are "on"). After one cycle, the number of "on" cells drops to 3, where it remains. It turns out that most networks with fixed and constant probabilities of turning "on" will reach a stable equilibrium -- usually within a few time steps (which depends, in part, on the diameter of the largest component of the graph).
It's a bit of work to set up network connections, and we don't have good visualizations yet. But you still should try a few experiments with the game of Life played in social network space, instead of physical space. Try to reason hypothetical answers to the questions above, and then construct simulations to test your hypotheses!
table of contentsThe range of social phenomena to which local or network density dependence models can be applied is quite broad. There are many interesting (and probably publishable) applications of the models in a number of sub-fields. Models for cascading failures, panics, crazes, fads, and social movement mobilization come immediately to mind.
There are also a number of things that one might reasonably want the models to do that they do not currently do. Here, we'll lay out just a few ideas of ways that these models might be developed to make them applicable to even broader classes of social dynamics.
For models of diffusion in neighborhoods, one could extend neighborhoods to use Euclidean distance, weighting the influences of neighbors inversely proportional to their distance (or some other function).
In models of diffusion in networks, one could include neighborhoods of path length greater than one. One could also use valued network weights. For example, actors might be more influenced by actors that, themselves, have more neighbors.
Actors could be simultaneously embedded in both spatial networks and social distance networks -- though hypothesizing rules for such a game could be challenging.
Probably more interesting, though, would be to create more complex "rules" of the game. One could make the rules themselves dynamic. Perhaps as the overall density of adoption in the grid increases, the values needed to sustain life in each neighborhood could become less. This could reflect a more complex hypothesis that conformity is enforced both by expectations expressed in face-to-face contact, as well as the expectations of the "generalized other."
Another very promising direction is to suppose that the population is not homogeneous in the rules (number of "on" neighbors or density of "on" neighbors) that govern their actions. Indeed, in any population there are likely to be actors who are more difficult to persuade, and more gullible. One could draw rules from various distributions, and assign them to actors either randomly, or by some design.
The game could also be made stochastic. That is, an increasing neighborhood density could increase the probability of turning "on" rather than deterministically "switching" at a cut-off value.
It need not be the case that actors are either "on" or "off." While a quite different mathematical approach (differential equations) would be needed, the degree of "on" could be modeled instead of the discrete state.
Even the simplest version of the game of Life is capable of producing some interesting dynamics. Without too much further complexity, it can be a useful research tool for exploring hypotheses about social change among connected actors.
table of contents